Intermediate 2nd Year Maths 2B Integration Formulas

 

Intermediate 2nd Year Maths 2B Integration Formulas

→ Integration is the inverse process of differentiation.

→ Let A ⊆ R and let f: A → R be a function. If there is a function B on A such that F'(x) = f(x), ∀ x ∈ A, then we call B an antiderivative of for a primitive of f.
i.e., ddx(sin x) = cos x, ∀ x ∈ R ax
f(x) = cos x, x ∈ R, then the function
F(x) = sin x, x ∈ R is an antiderivative or primitive of f.

→ If F is an antiderivative off on A, then for k ∈ R, we have (F + k) (x) = f(x), ∀ x ∈ A.

→ Hence F + k is also an antiderivative off.
∴ c is any real number F(x + c) = G(x) = sin x + c, ∀ x ∈ R is also an antiderivative of cos x.

→ It is denoted by ∫ (cos x) dx = sin x + c, (i.e.) ∫ f(x) dx = F(x) + c.

→ Here c is called a constant of integration,

f is called the integrand and x is called the variable of integration.

Intermediate 2nd Year Maths 2B Integration Formulas

Standard Forms:

→ ∫xn dx = xn+1n+1 + c if n ≠ – 1

→ ∫1x dx = log |x| + c

→ ∫ sin x dx = – cos x + c, x ∈ R

→ ∫ cos x dx – sin x + c, x ∈ R

→ ∫tan x dx = log |sec x| + c

→ ∫ cot x dx = log |sin x | + c

→ ∫sec x dx = log |sec x + tan x | + c (or) log |tan (π4+x2)| + c

→ ∫cosec x dx = log |cosec x – cot x| + c (or) log |tan(x2)| + c

→ ∫sec2 x dx = tan x + c, x ∈ R – ∣∣nπ2∣∣, n is odd integer

→ ∫cosec2 x dx = – cot x + c → R – nπ, n ∈ Z

→ ∫sec x tan x dx = sec x + c, R – [nπ2], n is an odd integer

→ ∫cosec x cot xdx = – cosec x + c, R – [nπ], n ∈ Z

→ ∫ex dx = ex + c, x ∈ R

→ ∫ax dx = 

logea + c, a > 0, a ≠ 1

→ ∫11+x2√ dx = sin-1x + C = – cos-1 (x) + c

→ ∫dx1+x2 dx = tan-1x + C = – cot-1 (x) + c

→ ∫dx|x|x2−1√ dx = sec-1x + C = – cosec-1 (x) + c

→ ∫ sinh x dx = cosh x + c

→ ∫cosh xdx = sinh x + c

→ ∫cosec2h x dx coth x + c

→ ∫sec2h x dx = tanh x + c

→ ∫cosech x coth xdx = – cosech x + c

→ ∫sech x tanh x dx = – sech x + c

→ ∫eax dx = eaxa + c

→ ∫eax+b dx = eax+ba + c

→ ∫sin (ax + b) dx = \frac{-\cos (a x+b)}{a} + c

→ ∫cos (ax + b) dx = sin(ax+b) + c

→ ∫sec2 (ax + b) dx = tan(ax+b) + c

→ ∫cosec2 (ax + b) dx = −cot(ax+b) + c

→ ∫cosec(ax + b) cot(ax + b) dx = −cosec(ax+b)a + c

→ ∫sec (ax + b) tan(ax + b) dx = sec(ax+b) + c

→ ∫f(x).g(x) dx = f(x) ∫g(x) dx – ∫[ddx f(x) . ∫ g(x) dx] dx (called as integration by parts)

→ ∫11+x2√ dx = sinh-1 (x) + c, x ∈ R = log (x + x2+1−−−−−√) + c, x ∈ R

→ ∫1x2−1√ dx = cosh-1 (x) + c (or) log (x + x2−1−−−−−√) + c, x ∈ (1, ∞)
= – cos h-1 (- x) + c (or) log (x + x2−1−−−−−√) + c, x ∈ (1, ∞)
= log |x + x2−1−−−−−√| + c, x ∈ R – [- 1, 1]

→ ∫ex [f(x) + f'(x)] dx = ex. f(x) + c

→ ∫1a2−x2√ dx = sin-1(xa) + c

→ ∫1a2+x2√ dx = sinh-1(xa) + c (or) log ∣∣x+x2+a2√∣∣a + c

→ ∫1x2−a2√ dx = cosh-1(xa) + c (or) log ∣∣x+x2−a2√∣∣a + c

→ ∫1a2+x2 dx = 1a tan-1(xa)+ c

→ ∫1a2−x2√ = 12a log ∣∣a+xa−x∣∣ + C

→ ∫1x2−a2 dx = 12a log ∣∣x−ax+a∣∣ + c

→ ∫a2−x2−−−−−−√ dx = 12x a2−x2−−−−−−√ + a22 sin-1(xa) + c

→ ∫x2+a2−−−−−−√ dx = 12x x2+a2−−−−−−√ + a22 sinh-1(xa) + c

→ ∫x2−a2−−−−−−√ dx = 12x x2−a2−−−−−−√ + a22 cosh-1(xa) + c

→ To evaluate

Intermediate 2nd Year Maths 2B Integration Formulas

• px+qax2+bx+c dx
• ∫ (px + q) ax2+bx+c−−−−−−−−−−√ dx
• ∫px+qax2+bx+c√ dx, where a, b, c, p, q ∈ R write
  px + q = A.ddx (ax2 + bx + c) + B and then integrate.

→ To evaluate ∫dx(ax+b)px+q√ where a, b, c, p, q, ∈ R put t2 = px + q

→ To evaluate ∫a+bcosx dx (or) a+bsinx dx
(or) a+bcosx+csinx dx, put tan x2 = t
Then sin x = 2t1+t2, cos x = 1−t21+t2 and dx = 21+t2 dt

→ To evaluate ∫acosx+bsinx+c dx where a, b, c, d e, f ∈ R; d ≠ 0, e ≠ 0, write a cos x + b sin x + c = A [d cos x + e sin x + f]’ + B (d cos x + e sin x + f) + ∨.
Find A, B, ∨ and then integrate.

→ If In = ∫xn . eax dx then In = xn⋅eaxa−na In – 1 for n ∈ N

→ If In = ∫ sinn (x) dx then In = – sinn−1(x)cosx + (n−1n) In – 2 for n ∈ N, n ≥ 2

→ f In = ∫ cosn (x) dx then In = – cosn−1(x)sinx + (n−1n) In – 2 for n ∈ N, n ≥ 2

→ If In = ∫tann (x) dx then In = tann−1(x) In – 2 for N ∈ n, n ≥ 2

→ If Im, n = ∫ sinm (x) cosn (x) dx then
If Im, n = 1m+n cosn – 1 (x) sinm + 1 (x) + (n−1m+n) Im, n – 2 where m, n ∈ N, n ≥ 2

→ If Im, n = ∫secn (x) dx then In = 

secn−2(x)tanx + (n−2n−1) In – 2

Intermediate 2nd Year Maths 2B Integration Formulas

Theorem: If f(x) and g(x) are two integrable functions then
∫ f(x).g(x)dx = f(x)∫g(x)dx – ∫f’(x)[∫g(x)dx] dx.
Proof:
ddx [f(x). ∫g(x)dx] = f(x) ddx[∫ g(x)dx] + ∫g(x)dx .ddx[f(x)]
= f(x)g(x) + [∫g(x)dx]f’(x)
∴ ∫[f(x)g(x) + f’(x)∫g(x)dx] dx = f(x)∫g(x)dx
⇒ ∫f (x)g(x)dx + ∫f’(x) [∫g(x)dx] dx = f (x)∫g(x) dx
∴ ∫f(x)g(x)dx = f(x)∫g(x)dx – ∫f’(x)[∫g(x)dx]dx

Note 1: If u and v are two functions of x then ∫u dv = uv – ∫v du.

Note 2: If u and v are two functions of x; u’, u”, u”’ …………. denote the successive derivatives of u and v1, v2, v3, v4, v5 … the successive integrals of v then the extension of integration by pairs is
∫uv dx = uv1 – u’v2 + u”v3 – u”’v4 + ………

Note 3: In integration by parts, the first function will be taken as the following order.
Inverse functions, Logarithmic functions, Algebraic functions, Trigonometric functions and Exponential functions. (To remember this a phrase ILATE).

Theorem: ∫eax cos bx dx = eaxa2+b2 (a cos bx + b sin bx) + c
Proof:

Intermediate 2nd Year Maths 2B Integration Formulas

Theorem: ∫eax sin bx dx = 

eaxa2+b2 (a sin bx – b cos bx)
Proof:
Let I = ∫eax sin bx dx = sin bx ∫eax dx – ∫[d(sin bx) ∫eax dx] dx

Intermediate 2nd Year Maths 2B Integration Formulas

Theorem: ∫ ex [f(x) + f’(x)]dx = exf(x) + c

Proof:
∫ex [f(x) + f’(x)]dx = ∫ex f(x)dx + ∫ex f’(x)dx
= f(x) ∫ exdx – ∫[d[f(x)] ∫exdx] dx + ∫ex f'(x)dx
= f(x)ex – ∫f'(x)exdx + ∫exf'(x) dx = exf(x) + c
Note: ∫e-x [f(x) – f’(x)]dx = – e-xf(x) + c

Definition: If f(x) and g(x) are two functions such that f’(x) = g(x) then f(x) is called antiderivative or primitive of g(x) with respect to x.

Note 1: If f(x) is an antiderivative of g(x) then f(x) + c is also an antiderivative of g(x) for all c ∈ R.

Definition: If F(x) is an antiderivative of f(x) then F(x) + c, c ∈ R is called indeVinite integral of f(x) with respect to x. It is denoted by ∫f(x)dx. The real number c s called constant of integration.

Note:

• The integral of a function need not exist. If a function f(x) integral then f(x) is called an integrable function.
• The process of finding the integral of a function is known as Integration.
• Integration is the reverse process of differentiation.

Corollary:
If f(x), g(x) are two integrable functions then ∫(f ± g) (x) dx = ∫f(x)dx ± ∫fg(x)dx

Corollary:
If f1(x), f2(x), ……, fn(x) are integrable functions then
∫(f1 + f2 + …….. + fn)(x)dx = ∫f1(x)dx + ∫f2(x)dx + ……. + ∫fn(x)dx.

Corollary:
If f(x), g(x) are two integrable functions and k, l are two real numbers then ∫(kf + lg) (x)dx = k∫f(x) dx + 1∫g(x)dx.

Intermediate 2nd Year Maths 2B Integration Formulas

Theorem: If f f(x)dx = g(x) and a ≠ 0 then ∫ f(ax + b)dx = 1ag(ax+b)+c.
Proof:
Put ax + b = t.

Intermediate 2nd Year Maths 2B Integration Formulas

Theorem: It f(x) is a differentiable function then ∫f′(x)f(x) dx = log |f(x)| + c.
Proof:
Put f(x) = t ⇒ f’(x) = dtdx ⇒ f’(x)dx = dt
∴ ∫f′(x)f(x) = ∫latex]\frac{1}{\mathrm{t}}[/latex] dt = log |t| + c = log |f(x)| + c

Theorem: ∫tan x dx = log |sec x| for x ≠ (2n + 1)π2, n ∈ Z.
Proof:
∫tan x dx = ∫sinx dx = -∫d(cosx) dx
= – log |cos x| + c = log|cosx| + c = log|sec x| + c

Theorem: ∫cot x dx = log |sin x| + c for x ≠ nπ, n ∈ Z.
Proof:
∫cot x dx = ∫cosx dx = log |sin x| + c

Intermediate 2nd Year Maths 2B Integration Formulas

Theorem: ∫ sec x dx = log |sec x + tan x| + c = log |tan(π/4 + x/2) + c for x ≠ (2n + 1)

π2, n ∈ Z.
Proof:

Intermediate 2nd Year Maths 2B Integration Formulas

Theorem: ∫csc x dx = log|csc x – cot x| + c = log |tan x/2| + c for x ≠ nπ, n ∈ Z.

Proof:
∫csc x dx = ∫cscx(cscx−cotx)cscx−cotx dx
= ∫csc2x−cscxcotxcscx−cotx dx = log |csc x – cot x| + c
= log∣∣1sinx−cosxsinx∣∣ + c
= log∣∣1−cosxsinx∣∣ + c
= log∣∣2sin2x/22sinx/2cosx/2∣∣ + c
= log |tan x/2| + c

Theorem: If f(x) is differentiable function and n ≠ – 1 then ∫[f(x)]n f’(x)dx = [f(x)]n+1n+1 + c.
Proof:
Put f(x) = t ⇒ f’(x) dx = dt

Theorem: If ∫f(x)dx = F(x) and g(x) is a differentiable function then ∫ (fog)(x)g’(x) dx = F[g(x)] + c.
Proof:
g(x) = t ⇒ g’(x) dx = dt
∴ ∫(fog)(x)g’(x)dx = ∫f[g(x)]g’(x) dx
= ∫f(t)dt = F(t) + c = F[g(x)] + c

Theorem: ∫

1a2−x2√ dx = Sin-1 + c for x ∈ (- a, a)
Proof:
Put x = a sin θ. Then dx = a cos θ dθ

Theorem: ∫1a2+x2√dx = Sinh-1  + c for x ∈ R.
Proof:
Put x = a sinhθ. Then dx = a cos hθ dθ
∴ ∫1a2+x2√ dx = ∫1a2+a2sinh2θ√ a coshθ dθ
= ∫acoshθ = ∫dθ = θ + c = Sinh-1(xa) + c

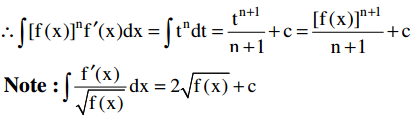Theorem:
∫dx = Cosh-1 + c for x ∈ (- ∞, – a) ∪ (a, ∞)
Proof:
Put x = a coshθ. Then dx = a sin hθ dθ
∴ ∫1x2−a2√ dx = ∫a2cosh2θ−a2 a sin hθ dθ
= ∫asinhθ dθ = ∫ dθ = θ + c = Cosh-1(xa) + c

Theorem:
∫1a2+x2 dx = 1a Tan-1(xa) + c for x ∈ R.
Proof:
Put x = a tan θ. Then dx = a sec2θ dθ

Theorem:

∫1a2−x2dx = 12a log∣∣a+xa−x∣∣ + c for x ≠ ± a
Proof:
∫1a2−x2dx = ∫∣∣a+xa−x∣∣dx
= 12a∫(1a+x+1a−x)dx = 12a [log |a + x| – log |a – x|] + c
= 12a log∣∣a+xa−x∣∣ + c

Theorem:
∫1x2−a2 dx = 12a log ∣∣x−ax+a∣∣ + c for x ≠± a
Proof:
∫1x2−a2 dx = ∫1(x−a)(x+a) dx
= 12a∫(1x−a−1x+a) dx = 12a [log |x – a| – log |x + a|] + c
= 12a log ∣∣x−ax+a∣∣ + c

Theorem:
∫a2−x2−−−−−−√dx = x2a2−x2−−−−−−√ + a22 sin-1(xa) + c for x ∈ (- a, a)
Proof:
Put x = a sin θ. Then dx = a cos θ dθ

Theorem:

∫a2+x2−−−−−−√ dx = x2a2+x2−−−−−−√ + a22 Sinh-1 (xa) + c for x ∈ R.
Proof:
Put x = sinhθ. Then dx = a coshθ dθ
∴ ∫a2+x2−−−−−−√ dx = ∫a2+a2sinh2θ a coshθ dθ
= ∫a1+sinh2θ−−−−−−−−√ a coshθ dθ = a2 ∫cosh2 θdθ
= =a2∫1+cosh2θ2 dθ=a22[θ+12sinh2θ]+c
= a22[θ+122sinhθcoshθ]+c
= a22[θ+sinhθ1+sinh2θ−−−−−−−−√]+c
= a22[Sinh−1(xa)+xa1+x2a2−−−−−√]+c
= a22Sinh−1(xa)+xaa2+x2−−−−−−√+c

Theorem:
∫x2−a2−−−−−−√ dx = x2x2−a2−−−−−−√ – a22 Cosh-1(xa) + c for x ∈ [a, ∞)
Proof:
Put x = a coshθ. Then dx = a sinhθ dθ

Intermediate 2nd Year Maths 2B Integration Formulas