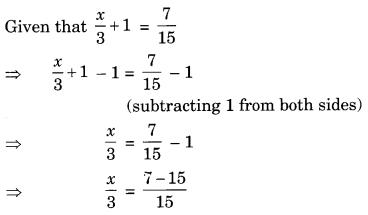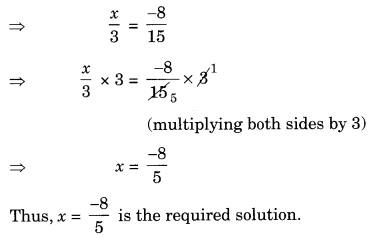Chapter 2 Linear Equations in One Variable Exercise 2.1
Ex 2.1 Class 8 Maths Question 1.
Solve the equation: x – 2 = 7.
Solution:
Given: x – 2 = 7
⇒ x – 2 + 2 = 7 + 2 (adding 2 on both sides)
⇒ x = 9 (Required solution)
Ex 2.1 Class 8 Maths Question 2.
Solve the equation: y + 3 = 10.
Given: y + 3 = 10
⇒ y + 3 – 3 = 10 – 3 (subtracting 3 from each side)
⇒ y = 7 (Required solution)
Ex 2.1 Class 8 Maths Question 3.
Solve the equation: 6 = z + 2
Solution:
We have 6 = z + 2
⇒ 6 – 2 = z + 2 – 2 (subtracting 2 from each side)
⇒ 4 = z
Thus, z = 4 is the required solution.
Ex 2.1 Class 8 Maths Question 4.
Solve the equations:
Solution:
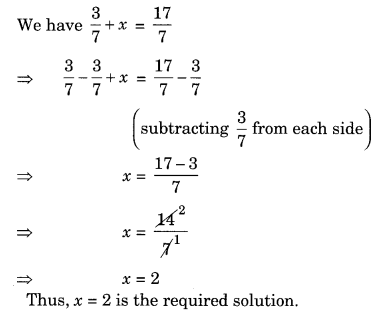
Ex 2.1 Class 8 Maths Question 5.
Solve the equation 6x = 12.
Solution:
We have 6x = 12
⇒ 6x ÷ 6 = 12 ÷ 6 (dividing each side by 6)
⇒ x = 2
Thus, x = 2 is the required solution.
Ex 2.1 Class 8 Maths Question 6.
Solve the equation
Solution:
Given
⇒
⇒ t = 50
Thus, t = 50 is the required solution.
Ex 2.1 Class 8 Maths Question 7.
Solve the equation
Solution:
We have
⇒
⇒ 2x = 54
⇒ 2x ÷ 2 = 54 ÷ 2 (dividing both sides by 2)
⇒ x = 27
Thus, x = 27 is the required solution.
Ex 2.1 Class 8 Maths Question 8.
Solve the equation 1.6 =
Solution:
Given: 1.6 =
⇒ 1.6 × 1.5 =
⇒ 2.40 = y
Thus, y = 2.40 is the required solution.
Ex 2.1 Class 8 Maths Question 9.
Solve the equation 7x – 9 = 16.
Solution:
We have 7x – 9 = 16
⇒ 7x – 9 + 9 = 16 + 9 (adding 9 to both sides)
⇒ 7x = 25
⇒ 7x ÷ 7 = 25 ÷ 7 (dividing both sides by 7)
⇒ x =
Thus, x =
Ex 2.1 Class 8 Maths Question 10.
Solve the equation 14y – 8 = 13.
Solution:
We have 14y – 8 = 13
⇒ 14y – 8 + 8 = 13 + 8 (adding 8 to both sides)
⇒ 14y = 21
⇒ 14y ÷ 14 = 21 ÷ 14 (dividing both sides by 14)
⇒ y =
⇒ y =
Thus, y =
Ex 2.1 Class 8 Maths Question 11.
Solve the equation 17 + 6p = 9.
Solution:
We have, 17 + 6p = 9
⇒ 17 – 17 + 6p = 9 – 17 (subtracting 17 from both sides)
⇒ 6p = -8
⇒ 6p ÷ 6 = -8 ÷ 6 (dividing both sides by 6)
⇒ p =
⇒ p =
Thus, p =
Ex 2.1 Class 8 Maths Question 12.
Solve the equation
Solution: